My last post about implementing a turn based game ai became famous on Reddit/Programming for one day. It looks like many developers are interested in this topic. Some readers, with more knowledge of the topic than myself, have added interesting insight that I would like to share with you here. If you haven’t read the first post, you might want to have a look there first.

Minimax algorithm

The algorithm that I presented is called Minimax and is famous in academia for creating turn based game AIs. It has this name, because one player tries to minimize the getValue() result and another player tries to maximize it.

For improving the AI strength you either have to improve your getValue() function, or increase the size of your decision tree. Usually, getValue() can only be improved to a certain point which is far from perfect. Therefore, at some point you want to focus on increasing the tree size. This means looking more half-moves into the future.

We can increase the tree size simply by using a higher recursionDepth value. It depends on your game, which value is good enough for a strong computer AI. Laska is using a recursionDepth value of 4 for the strong computer player, 2 for medium and only 1 on easy. This is good enough, because I want my users to win most of the time. I want them to enjoy beating a hard computer opponent if they are good players.

If your AI should be more competitive, you need a higher recursionDepth. The problem is, that you will soon have a high runtime complexity and calculation time. If we have a Branching Factor of b and a recursionDepth of d, we have a complexity of O(b^d). So let’s say Laska has 4 possible moves on average and I am using a depth of 4. Then my AI is crunching through 4^4 = 256 situations, calculating and comparing their value. This is not very much and also the reason I never had to optimize.

On the other hand, if you are implementing a chess AI the branching factor is 35. There is much more competition in this game and you might want to have a depth of 8. Then you are looking at 35^8 = 2.251.875.390.625 situations, which obviously is too much.

Alpha-Beta Pruning

In this case you should focus on further optimizations. The most important is called alpha-beta pruning. It will cut off subtrees whenever they can not influence the root decision (making a single half-move) anymore.

When can this happen? Every move could turn around the game instantly. In chess, you could be way behind in everything regarding your getValue() and still make a checkmate within a few moves. So how can you ever discard a whole subtree?

It is true that at some point you have to consider every possible move. However, when we know there is a winning path, we don’t need to figure out if there are more in this subtree. If we have a winning path down the tree, we just start with the first move. This goes both ways. If we have a path that definitely gives us a loss, our opponent will choose exactly that path.  We don’t need to evaluate any other moves from his side.

This is not restricted to winning moves. If we have already found out, that move 1 gives us a minimum value of 5 we can use this knowledge and stop evaluating move 2 once we know it is worse. We know move 2 is worse when our opponent can force it to a value below 5 with optimal moves on his side. This is best described in the following gif from Wikipedia:

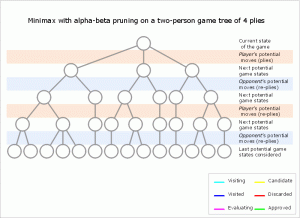
On the left side we have the situation described above. The rows in red mark red moves and the ones in blue stand for blue moves. Blue is minimizing the value, while red is maximizing it. So on the lower left side, when blue has to choose between 5 and 6, we know that he will choose 5. In the next subtree, blue can choose between 7, 4 and something else. We can already stop at 4, because whatever number comes, this is already the preferable subtree for blue. We don’t need the correct value, as long as we still get the optimal move.

Alpha-beta pruning makes a huge difference when the decision tree is large. According to this link, it reduces the number of leaves to the square root. So if we use the previous example with 2.251.875.390.625 leaves, we only have to check 1.500.625 situations. That is still a high number, but not impossible anymore.

Example Code in Laska

So how does the alpha-beta pruning look in a game like Laska?

public Move bestMove(int recursionDepth) {
	int maxValue = -SOME_HIGH_NUMBER;
	Move bestMove = null;
	Vector<Move> possibleMoves = field.getPossibleMovesOfActivePlayer();
	if (possibleMoves.size() > 1) {
		for (Move move : possibleMoves) {
			LaskaField nextField = getNextField(field, move);
			int value = -alphaBeta(nextField, maxValue, SOME_HIGH_NUMBER, recursionDepth - 1);
			if (bestMove == null || value > maxValue || (value == maxValue && new Random().nextInt(2) == 1)) {
				maxValue = value;
				bestMove = move;
			}
		}
	} else {
		bestMove = possibleMoves.firstElement();
	}
	return bestMove;
}

The bestMove() method still looks much like the old version. It now calls alphaBeta() instead of getValueOfMove(), but both will return the value of a given move. The alphaBeta() value is negated and the method takes parameters for alpha and beta, in this case +/-SOME_HIGH_NUMBER.

public int alphaBeta(LaskaField currentField, int alpha, int beta, int depthleft) {
	if (depthleft == 0) {
		int value = currentField.getValue(currentField.activePlayer);
		value -= currentField.getValue(1 + (currentField.activePlayer % 2));
		return value;
	}
	Vector<Move> possibleMoves = currentField.getPossibleMovesOfActivePlayer();
	if (possibleMoves.size() == 0) {
		return -1000;
	}
	for (Move move : possibleMoves)  {		LaskaField nextField = getNextField(currentField, move);
		int score = -alphaBeta(nextField, -beta, -alpha, depthleft - 1);
		if (score >= beta)
			return beta; 
		if (score > alpha)
			alpha = score;
	}
	return alpha;
}

Also alphaBeta() didn’t change too much. At first, there is the recursion termination. When depthleft equals 0, we just calculate the current value and return it.

If we are not in a leave node we calculate all possible moves. If there is none, the current player has lost the match and we can return a -1000 here. Otherwise we continue walking through the tree. Just this time we pass parameters for alpha and beta.

Alpha notes the highest value of a move we are interested in and beta the lowest. If the current move has a score higher than beta, we can prune the graph here and stop calculating further, because the other player will not let us make this move. Otherwise, if the score is higher than alpha, we have found a better move and need to save it.

Runtime comparison

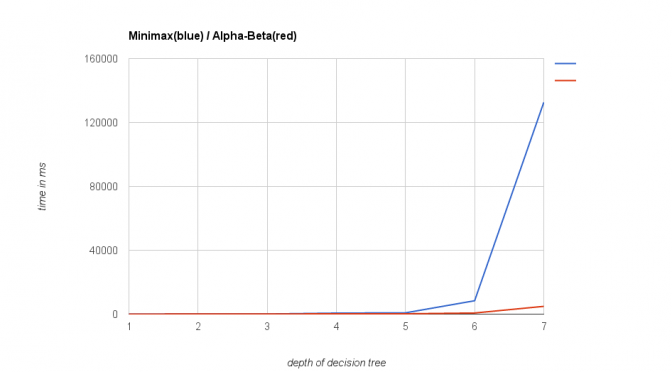
To see how much the alpha-beta pruning impacts performance, I ran a test case with the old algorithm playing against the new version with increasing depths of the decision tree. In the following diagram you see the time used for playing a complete game (up to 100 moves or until we have a winner).

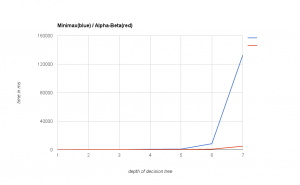
As you can see, there is no visible difference for depths up to 5. Alpha-Beta is considerably faster at depth 6 and it totally owns Minimax on depths greater than this.

Further improvements

While this improvement is dramatic for higher depth levels, we can still do much better. Some further improvements are independent from your game, some depend on special knowledge about it and others trade a little accuracy for increasing the depth of your tree.

The next optimization you might want to look into is ordering of moves for improving alpha-beta pruning. How you order your possible moves impacts how well the alpha-beta algorithm prunes the graph. If you start with best moves first, it can cut off more of the tree later on.

There is a great overview of further improvements on StackOverflow. You can dedicate a lot of time to this. However, don’t forget to check if your algorithm is already good enough. Because if the main task is not beating Garry Kasparov, you probably should improve user experience, design, marketing, etc.. first.